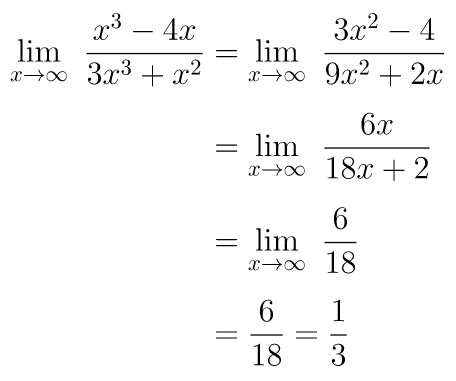www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Limit ›
Hitunglah \( \displaystyle \lim_{x \to \infty} \ \frac{x^3 - 4x}{3x^3+x^2} \).
Pembahasan:
Dengan memasukkan \(x = \infty\) ke fungsi limitnya diperoleh bentuk tak tentu ∞/∞ sehingga Aturan L'Hospital dapat dipakai untuk menangani limit ini.
Perhatikan bahwa pembilang dari fungsi limitnya yaitu \(x^3-4x\) di mana turunan pertamanya yaitu \(3x^2 - 4\), turunan keduanya \(6x\), dan turunan ketiganya yaitu 6. Sementara itu, penyebut dari fungsi limitnya yaitu \(3x^3 + x^2\) di mana turunan pertama, kedua, dan ketiganya berturut-turut yaitu \(9x^2+2x, \ 18x+2, \ 18\).
Dengan demikian, menurut Aturan L'Hospital, kita peroleh:
